Пусть \((t_0,x_0)\in \Gamma\). Область \(\Gamma\) открытое множество и \((t_0,x_0)\) содержится в \(\Gamma\) вместе с некоторой своей окрестностью.
Рассмотрим \[{D_r=\{(t,x)\in R^2:|t-t_0|\leq r,\; |x-x_0|\leq a\}},\] \(D_r\) - компакт (является ограниченным и замкнутым) в \(\Gamma\). Функции \(f(t,x)\) и \(f'_x(t,x)\) непрерывны в \(\Gamma\) значит \[\exists\quad K,M>0\quad\forall (t,x)\in D_r\quad |f(t,x)|\leq K,\quad |f'_x(t,x)|\leq M.\]
Обозначим \[{D_q=\{(t,x)\in R^2:|t-t_0|\leq q,\; |x-x_0|\leq a\}},\] \[D_q\subset D_r,\quad 0 < q\leq r.\] Обозначим \[G_q=\{x(\cdot)\in C(t_0-q,t_0+q):\quad |x-x_0|\leq a\ \quad\forall t\in [t_0-q,t_0+q]\; \},\]
\(G_q\) - подпространство пространства \[C=C(t_0-q,t_0+q)\] непрерывных функций \(\{x(\cdot)\}\), заданных на отрезке \([t_0-q,t_0+q]\) c метрикой \[\rho[x_1(\cdot),x_2(\cdot)]=\max\limits_{\tau\in [t_0-q,t_0+q]} |x_1(\tau)-x_2(\tau)|.\] Графики функций не выходят за пределы прямоугольника \(D_q\). Очевидно, \(\forall x(\cdot) \in G_q\) справедливо неравенство \(|x(t)-x_0|\leq a\).
\(1.\) \(G_q\) - замкнуто. Надо показать, что \[\forall \quad\{x_n(\cdot)\}\in G_q :\quad x_n(t)\rightarrow x(\cdot),\quad n\to\infty\] следует, что и \(x(\cdot)\in G_q.\)
\(\bullet \) Сходимость в пространстве \(C\) является равномерной, следовательно предельная функция \(\hspace{0.5cm}\) \(x(\cdot)\) непрерывна, т.е. \(x(\cdot)\in C(t_0-q,t_0+q).\)}
\(\hspace{0.5cm} \bullet \) Переходя к пределу при \(n\to\infty\) в неравенстве \(|x_n(t)-x_0|\leq a\) получим \(\hspace{0.5cm} |x(t)-x_0|\leq a\).
Значит \(x(\cdot)\in G_q.\) Замкнутость \(G_q\) доказана.
Из замкнутости \(G_q\) вытекает полнота \(G_q\) как метрического пространства.
\(2.\) Введем на множестве \(G_q\) оператор \(A:G_q\to G_q\)
\[A(x(\cdot))=x^*(\cdot), \]
\[\forall t \in [t_0-q,t_0+q] \quad x^*(t)=x_0+\int\limits_{t_0}^tf[\tau,x(\tau)]\,d\tau.\]
Покажем, что \(A\) \(\textbf{сжимающий}\) на \(G_q\). Надо показать:
1)Если \(x(\cdot)\in G_q,\) то \(x^*(\cdot)\in G_q;\)
2)Если \(x_1(\cdot), x_2(\cdot)\in G_q,\) то
\[\rho [x^*_1(\cdot), x^*_2(\cdot)]\leq k\rho [x_1(\cdot), x_2(\cdot)],\] где
\( 0 < k < 1. \)
1) Действительно, \(x^*(t)\in C(t_0-q,t_0+q)\). Далее
\[|x^*(t)-x_0|=|\int_{t_0}^tf[\tau,x(\tau)]\,d\tau|\leq \]
\[\leq |\int_{t_0}^t|f[\tau,x(\tau)]|\,d\tau|\leq K|t-t_0|\leq Kq.\] Чтобы выполнялось равенство \(|x^*(t)-x_0|\leq a\) нужно выбрать \(q\) таким, что \(Kq\leq a\), т.е. считать, что
\[q\leq \frac{a}{K}.\]
2) Пусть \(x_1(t), x_2(t)\in G_q\).
\begin{equation}\label{1}
\left|x_1^*(t)-x_2^*(t)\right|=\left|\int\limits_{t_0}^tf\left[\tau,x_1(\tau)\right]\,d\tau-\int\limits_{t_0}^tf\left[\tau,x_2(\tau)\right]\,d\tau\right|
\leq \left|\int\limits_{t_0}^t\left|f\left[\tau,x_1(\tau)\right]-f\left[\tau,x_2(\tau)\right]\right|\,d\tau\right|.
\end{equation}
По формулe конечных приращений Лагранжа
\begin{equation}\label{2}
f\left[\tau,x_1(\tau)\right]-f\left[\tau,x_2(\tau)\right]=f'_x(\tau,\theta_\tau)\left[x_1(\tau)-x_2(\tau)\right],
\end{equation}
\[x_1(\tau)\leq\theta_\tau\leq x_2(\tau),\quad (\tau,\theta_\tau)\in D_q,\]
\[{\left|f'_x(\tau,\theta_\tau)\right|\leq M}\;\;\left({\forall\tau\in[t_0-q,t_0+q]}\right).\]
Из (\ref{1})-(\ref{2}) для \(t:|t-t_0|\leq q\)
\begin{equation}\label{3}
\left|x_1^*(t)-x_2^*(t)\right|\leq \left|\int\limits_{t_0}^tM\left|x_1(\tau)-x_2(\tau)\right|\,d\tau\right|\leq M|t-t_0|\times\\
\hspace{3cm}\times \max_{t_0-q\leq \tau \leq t_0+q} \left|x_1(\tau)-x_2(\tau)\right|\leq Mq\rho\left[x_1(\cdot),x_2(\cdot)\right].
\end{equation}
Окончательно,
\[\rho\left[x_1^*(\cdot),x_2^*(\cdot)\right]=\max_{t_0-q\leq \tau \leq t_0+q} \left|x_1^*(\tau)-x_2^*(\tau)\right|\leq Mq\rho\left[x_1(\cdot), x_2(\cdot)\right]\] или
\[\rho\left[A(x_1(\cdot)),A(x_2(\cdot))\right]\leq Mq\rho\left[x_1(\cdot),x_2(\cdot)\right].\]
В итоге, если взять \(q\), такое, что
\[0\leq q \leq r,\quad q\leq\frac{a}{K},\quad q\leq\frac{1}{M}\] то выполняется \[\rho [x^\ast_1(\cdot), x^\ast_2(\cdot)]\leq k\rho [x_1(\cdot), x_2(\cdot)], \hspace{0.5cm} k=q, \hspace{0.5cm} 0 < k < 1.\]
Оператор \(A\) сжимающий.
Согласно принципу сжатых отображений существует и единственно \(\varphi(\cdot)\in G_q\) (в окрестности точки \((t_0,x(t_0)\))
\[A(\varphi(\cdot))=\varphi(\cdot), \varphi(t)=x_0+\int\limits_{t_0}^tf\left[\tau,\varphi(\tau)\right]\,d\tau,\quad t\in[t_0-q,t_0+q].\]
По лемме функция \(\varphi(t)\) является решением задачи Коши.
Теорема доказана.
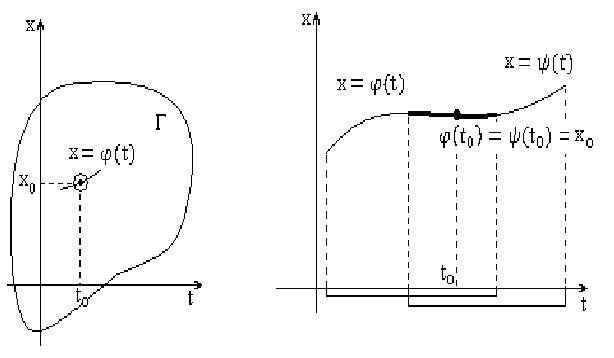
Была доказана локальная теорема Коши. Единственность решения установлена в некоторой окрестности \((t_0,x_0).\) Это \(\textbf{локальная}\) единственность. Т.е., если два решения \(x_1(t)\) и \(x_2(t)\) совпадают при \(t=t_0\), то они совпадают и в некоторой окрестности этой точки.
В условиях теоремы можно доказать свойство \(\textbf {глобальной}\) единственности.
Пусть \(x_1(t)\) и \(x_2(t)\) - решения уравнения и \(x_1(t_0)=x_2(t_0)=x_0\). Обозначим \((\alpha,\beta)\) --- интервал их совместного определения (пересечение областей определения). Надо доказать, что \(\forall t\in (\alpha,\beta)\; x_1(t)=x_2(t).\)
От противного, предположим существует значение \(t=t^*\in(\alpha,\beta)\) и \(x_1(t^*)\neq x_2(t^*).\)
Ограничимся случаем, когда \(t^* > t_0\) (аналогично можно рассмотреть случай \(t^* < t_0\) ).
Рассмотрим множество
\[T=\{\tau\in [t_0,t^*]:x_1(\tau)=x_2(\tau)\}.\]
Множество \(T\) \(\textbf{не пусто}\), \(t_0\in T\).
Множество \(T\) \(\textbf{замкнуто}\). Действительно. Пусть для любого \(n\) \(\tau_n\in T\) и \(\tau_n\rightarrow\hat{\tau}.\)
Так как \(\tau_n\in [t_0,t^*]\), то и \(\hat{\tau}\in [t_0,t^*].\) Далее, в силу непрерывности функций \(x_1(\tau)\), \(x_2(\tau_n)\) при \({n\rightarrow\infty}\) в равенстве \(x_1(\tau_n)=x_2(\tau_n)\) имеем
\[x_1(\hat{\tau})=x_2(\hat{\tau}).\] Значит \(\hat{\tau}\in T\). Замкнутость доказана.
Множество \(T\) имеет точную верхнюю границу. Обозначим
\[\overline{\tau}=\sup T.\] В силу определения и замкнутости \(T\) имеем \(\overline{\tau}\leq t^*\) и \(\overline{\tau}\in T\). Точнее \(\overline{\tau}< t^*\). (Равенства нет, поскольку \(x_1(\overline{\tau})=x_2(\overline{\tau})\) и по предположению \(x_1(t^*)\neq x_2(t^*)\).)
Согласно локальной единственности для \(\overline{\tau}< t^*\)
\[\exists \delta>0\quad \forall \tau \in (\overline{\tau}-\delta,\overline{\tau}+\delta)\quad x_1(\tau)=x_2(\tau),\] что противоречит определению \(\overline{\tau}\):
\[\forall \tau\in (\alpha,\beta):\tau>\overline{\tau}\quad \Rightarrow \quad x_1(\tau)\neq x_2(\tau).\]
Следовательно, таких точек \(t^*\in (\alpha,\beta)\) не существует.
Глобальная единственность доказана.
В доказанной теореме условие существования \(f'_x(t,x)\) и ее непрерывности можно заменить на условие Липшица: для любого ограниченного замкнутого подмножества \(D\subset \Gamma\) существует число \[L>0:\forall (t,x_1),(t,x_2)\in D\quad |f(t,x_1)-f(t,x_2)|\leq L |x_1-x_2|.\]
Можно показать, что для существования решения задачи Коши достаточно только непрерывности функции \(f(x,y)\) в области \(\Gamma\). При этом частные производные \(f'_x(t,x)\) могут не существовать или не являться непрерывными. Условие непрерывности \(f'_x(t,x)\) в теореме обеспечивает единственность.